- Sea
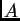 una de las paredes de un recipiente que contiene un gas
ideal. Consideramos el espacio reportado al triedro directo
una de las paredes de un recipiente que contiene un gas
ideal. Consideramos el espacio reportado al triedro directo
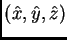 , en que
, en que 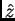 es paralelo a la normal
en la pared
es paralelo a la normal
en la pared 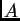 . Encuentre el número de partículas que chocan
en un tiempo
. Encuentre el número de partículas que chocan
en un tiempo 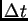 en
en 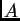 , con velocidades orientadas en
direcciones que forman un ángulo con el eje
, con velocidades orientadas en
direcciones que forman un ángulo con el eje 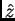 entre
entre 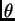 y
y
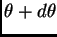 (coordenadas esféricas), y con modulo de
velocidades entre
(coordenadas esféricas), y con modulo de
velocidades entre  y
y
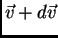 .
.
- Deduzca la ley de gas ideal
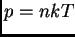 calculando la presión
ejercida sobre la pared, suponiendo que las partículas chocan
elásticamente con la pared.
calculando la presión
ejercida sobre la pared, suponiendo que las partículas chocan
elásticamente con la pared.
- Consideramos ahora una compresión/dilatación adiabática
del gas, en que la pared
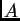 es ahora un pistón que se mueve con
velocidad
es ahora un pistón que se mueve con
velocidad 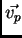 mucho menor que cualquiera de las velocidades
de las partículas.
mucho menor que cualquiera de las velocidades
de las partículas.
- Muestre que la cantidad de energía perdida por el gas en el
choce de una partícula de masa
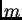 con la pared es
con la pared es

en el sistema de referencia ligado al laboratorio (ayuda: en el sistema ligado al pistón, el choque es elástico, y haga explicita la hipotesis adiabática). - Sumando sobre todas las partículas que chocan con el
pistón en un tiempo
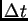 , muestre que la cantidad de
energía perdida por el gas es
, muestre que la cantidad de
energía perdida por el gas es
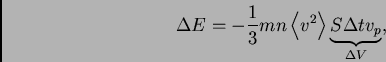
en que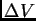 es el incremento de volumen en
el tiempo
es el incremento de volumen en
el tiempo 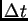 .
.
- Ligue la relación deducida anteriormente con la energía
total del gas, y llegue a

- Demuestre que en la compresión adiabática de un gas ideal
tenemos la relación

- Muestre que la cantidad de energía perdida por el gas en el
choce de una partícula de masa
Ecuación de estado y energía total de un gas ideal en un campo de energía potencial.
Consideramos un volumen ![]() con un gas ideal, en el cual las
partículas se mueven con energía potencial nula, salvo por
unas zonas en las cuales adquieren una cierta energía potencial
con un gas ideal, en el cual las
partículas se mueven con energía potencial nula, salvo por
unas zonas en las cuales adquieren una cierta energía potencial
![]() . El tamaño y la forma de las zonas de alta energía
potencial es cualquiera, y el volumen total ocupado por estas zonas es
una fracción
. El tamaño y la forma de las zonas de alta energía
potencial es cualquiera, y el volumen total ocupado por estas zonas es
una fracción ![]() del
del ![]() . Se pide mostrar que la energía total
media del gas es,
. Se pide mostrar que la energía total
media del gas es,
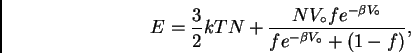
y explicar físicamente por qué si