Next: About this document ...
2
Problemas, termodinámica estadística
Temperatura y entropía.
Considere un sistema 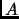 , con energía
, con energía 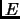 , entropía
, entropía
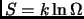 y
y 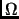 estados igualmentes probables, en equilibrio
con un reservorio de temperatura
estados igualmentes probables, en equilibrio
con un reservorio de temperatura 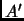 . Si la temperatura es
. Si la temperatura es
demostrar que el valor mas probable de 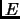 corresponde al máximo de
entropía de
corresponde al máximo de
entropía de
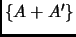 , que
, que
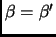 , y
calcular la probabilidad que
, y
calcular la probabilidad que 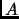 esté en un cierto estado
esté en un cierto estado 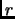 con
energía
con
energía 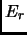 . Si
. Si 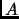 es un gas ideal, calcule la energía
media de una de sus
es un gas ideal, calcule la energía
media de una de sus 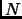 moléculas, y compare con
moléculas, y compare con
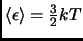 .
Entropía de un gas ideal.
Mostrar que para un gas ideal,
.
Entropía de un gas ideal.
Mostrar que para un gas ideal,
y que la diferencia de entropía entre dos estados 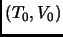 y
y
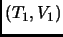 es
es
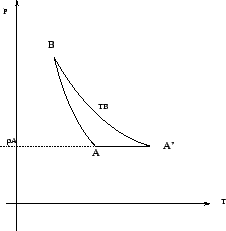
Para ello graphique en un diagrama 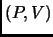 dos ejemplos de processos que permiten unir los puntos
dos ejemplos de processos que permiten unir los puntos
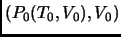 y
y
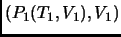 . Ver que
. Ver que
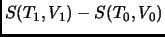 es simplemente la diferencia entre la entropía
evaluada en dos puntos, y que no depende de proceso específico
que lleva el sistema de
es simplemente la diferencia entre la entropía
evaluada en dos puntos, y que no depende de proceso específico
que lleva el sistema de 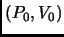 a
a 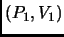 (en otras palabras,
la entropía es una función de estado).
Compresión y expansión isotermal de un gas ideal
(en otras palabras,
la entropía es una función de estado).
Compresión y expansión isotermal de un gas ideal
- Considere el proceso isotermal (o sea en contacto con un
reservorio de temperatura) que lleva un gas ideal de un volumen
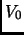 a un volumen
a un volumen 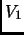 . Calcular
. Calcular
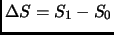 , y graficar el
proceso por una linea en un diagrama
, y graficar el
proceso por una linea en un diagrama 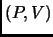 . Demarcar el área en el
diagrama que corresponde al trabajo realisado en la compresión. Cual
es la variación en energía interna? Cuanto calor recibió el
gas ideal?
. Demarcar el área en el
diagrama que corresponde al trabajo realisado en la compresión. Cual
es la variación en energía interna? Cuanto calor recibió el
gas ideal?
- La diferencia de entropía entre los puntos
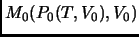 y
y
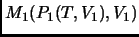 no depende del camino
que los una en el diagrama
no depende del camino
que los una en el diagrama 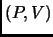 . Pero el trabajo ejercido sobre el
gas ideal si depende del camino. Considere ahora un proceso
isobárico seguido por un proceso isocórico, que unen los puntos
. Pero el trabajo ejercido sobre el
gas ideal si depende del camino. Considere ahora un proceso
isobárico seguido por un proceso isocórico, que unen los puntos
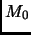 y
y 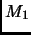 . Calcule, y grafique, el trabajo ejercido sobre el
sistema en este caso, y calcule la diferencia de entropía
integrando sobre este nuevo camino.
. Calcule, y grafique, el trabajo ejercido sobre el
sistema en este caso, y calcule la diferencia de entropía
integrando sobre este nuevo camino.
- Considere ahora la expansión adiabática y libre de un gas
ideal aislado, en el cual se aumenta bruscamente el volumen. El gas no
está en equilibrio durante la expansión, y por lo tanto no puede
representarse el estado transitorio por puntos en el diagrama
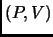 .
Cual es la variación de energía interna al pasar de un volumen
.
Cual es la variación de energía interna al pasar de un volumen
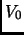 a
a 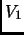 ? Cual es la variación en temperatura? Cual es la
variación de entropía? Este proceso es reversible? (ayuda:
convencerse de que en la expansión libre no hay fuerza que retenga
la pared, y por lo tanto el trabajo ejercido por el gas es cero, y use
los dos puntos anteriores).
? Cual es la variación en temperatura? Cual es la
variación de entropía? Este proceso es reversible? (ayuda:
convencerse de que en la expansión libre no hay fuerza que retenga
la pared, y por lo tanto el trabajo ejercido por el gas es cero, y use
los dos puntos anteriores).
Aumento de entropía al llevar dos sistemas en
equilibrio térmico
Considere un sistema 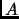 con volumen constante a temperatura
con volumen constante a temperatura 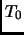 con
capacidad calórica
con
capacidad calórica 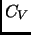 en contacto con un reservorio
en contacto con un reservorio 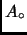 a
temperatura
a
temperatura 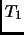 . Mostrar que al concluir el proceso que lleva los
dos sistema al equilibrio, el aumento de entropía del sistema
. Mostrar que al concluir el proceso que lleva los
dos sistema al equilibrio, el aumento de entropía del sistema
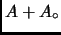 es
es
y que 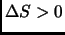 .
.
Transformaciones sobre un gas ideal
Consideramos un mol de gas ideal, con ecuación de estado 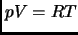 (
(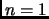 , el número de moles), cuya energía interna es
, el número de moles), cuya energía interna es
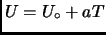 , donde
, donde 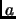 es una constante positiva.
es una constante positiva.
- Expresar la entalpía
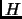 en función de
en función de 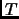 ; determinar los
valores de
; determinar los
valores de 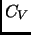 y
y 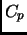 (recuerde que
(recuerde que
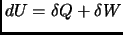 , y que
, y que
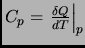 ).
).
- Partiendo de un estado de equilibrio inicial
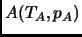 ,
sometemos este mol a diversas transformaciones reversibles:
,
sometemos este mol a diversas transformaciones reversibles:
- Representar las transformaciones
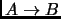 y
y
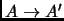 en un diagrama
en un diagrama 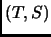 . Escribiendo de dos
maneras distintas el diferencial
. Escribiendo de dos
maneras distintas el diferencial 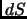 de
de 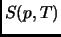 , determinar
, determinar
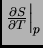 ; deducir y dibujar
la pinta de la curva que representa la transformación de
; deducir y dibujar
la pinta de la curva que representa la transformación de
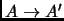 .
.
- Partiendo ahora del estado de equilibrio
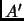 aplicamos
bruscamente a este mol la presión
aplicamos
bruscamente a este mol la presión 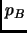 , manteniendolo en contacto
con un reservorio a temperatura
, manteniendolo en contacto
con un reservorio a temperatura 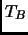 . Cuando el nuevo equilibrio se
establece, cual es el punto que representa el estado del gas?
Expresar la cantidad de trabajo
. Cuando el nuevo equilibrio se
establece, cual es el punto que representa el estado del gas?
Expresar la cantidad de trabajo 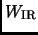 y de calor
y de calor
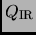 intercambiados con el medio externo en esta
transformación. Cual es la variación de entropía del mol?
intercambiados con el medio externo en esta
transformación. Cual es la variación de entropía del mol?
- Escribir la expresión del diferencial
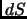 en función de
en función de
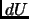 y de
y de 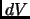 . Usando la ecuación de estado y de energía
interna, encontrar una expresión para
. Usando la ecuación de estado y de energía
interna, encontrar una expresión para 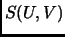 de un mol de
gas. Deducir una expresión para el número de microestados
de un mol de
gas. Deducir una expresión para el número de microestados
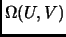 .
.



Next: About this document ...
simon
2002-09-13
![]() , con energía
, con energía ![]() , entropía
, entropía
![]() y
y ![]() estados igualmentes probables, en equilibrio
con un reservorio de temperatura
estados igualmentes probables, en equilibrio
con un reservorio de temperatura ![]() . Si la temperatura es
. Si la temperatura es ![]() con volumen constante a temperatura
con volumen constante a temperatura ![]() con
capacidad calórica
con
capacidad calórica ![]() en contacto con un reservorio
en contacto con un reservorio ![]() a
temperatura
a
temperatura ![]() . Mostrar que al concluir el proceso que lleva los
dos sistema al equilibrio, el aumento de entropía del sistema
. Mostrar que al concluir el proceso que lleva los
dos sistema al equilibrio, el aumento de entropía del sistema
![]() es
es ![]() (
(![]() , el número de moles), cuya energía interna es
, el número de moles), cuya energía interna es
![]() , donde
, donde ![]() es una constante positiva.
es una constante positiva.