Diagramas de Espacio-Tiempo.

Referencia: Herbert Massmann, 1988, ``Escuela de Talentos I, Introducción a la Teoría de la Relatividad Especial'', Biblioteca Central Fac. de Ciencias.

I Espacio-Tiempo, versión Galileana.

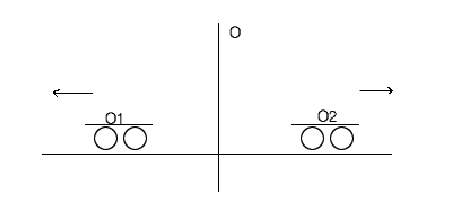
Considerar la siguiente situación:

Los observadores O$_1$ y O$_2$ se mueven con la misma velocidad $v/2$ y con direcciones opuestas con respecto al observador O, que se distingue formalmente como el observador estacionario. Para fijar ideas, O es una estación de trenes, mientras que O$_1$ y O$_2$ son trenes que se van alejando. Supongamos que O$_1$ y O$_2$ partieron en $t=0$ desde el orígen del sistema de coordenadas ligado a O.

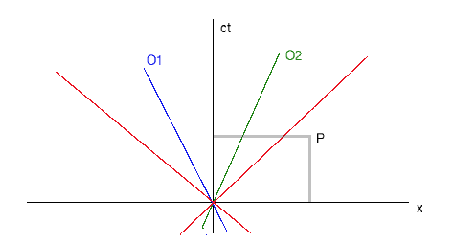
La Figura 1 muestra el espacio-tiempo de O. Para leer las coordenadas del evento $P$ en esta figura, dibujamos lineas paralelas a los ejes temporales y espaciales. P tiene coordenas $(x,ct)$ Para poder comparar el eje de los tiempos con el eje espacial, hemos multiplicado los tiempos por una velocidad, en este caso $c$. Las lineas verdes y azules corresponden a las lineas de mundos de O$_1$ y O$_2$. Los ángulos $\widehat{(ct,O_1)}$ y $\widehat{(ct,O_2)}$ son iguales, y los podemos calcular usando un evento en la linea de mundo de O$_2$, digamos $E(x_E,ct_E)$. Si $\alpha=\widehat{(ct,O_1)}$, $\tan \alpha = x_E/ct_E = v/2c$.

Figura 1: El espacio tiempo de O. Rayos de luz emitidos en $x=0$, $t=0$, estan graficados en rojo - corresponden a las bisectrices de los ángulos $\widehat{(ct,x)}$.

Imagenimos que asignamos escalas de unidades a las lineas de mundo de O$_1$ y O$_2$, respectivamente $ct_1$ y $ct_2$, de tal forma que la linea horizontal que proyecta el evento P sobre el eje $ct$ cruce las lineas $ct_1$ y $ct_2$ con $t_1=t_2=t$. Como las distancias desde el orígen hasta $ct_1$ y $ct_2$ son las mismas, las unidades en los ejes O$_1$ y O$_2$ son las mismas, pero son distintas de las de O. Vemos que con la introducción de estos ejes que la linea de mundo de O$_2$ es su propio eje temporal: un evento que le ocurre a O$_2$ (por ejemplo aterriza una mosca en la nariz del chofer del tren), tiene coordenada $x_2 =0$.

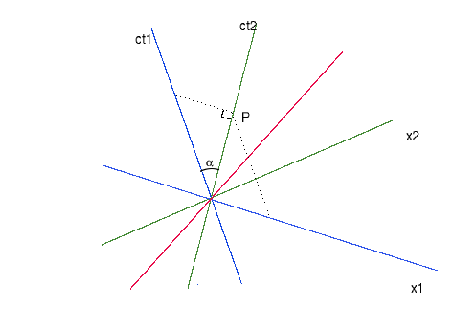
La Figura 2 muestra como medir las coordenadas de un evento P para los espacios-tiempos de O$_1$ y O$_2$, con lineas paralelas a los ejes espaciales y temporales. Si queremos usar este sistema en para describir los espacio-tiempos de ambos observadores en el mismo grafico, debemos revisar las unidades de los ejes y el ángulo $2\alpha=\widehat{(ct_1,ct_2)}$. Elegimos iguales las unidades de $ct$ y de $x$. Vemos ahora que, para que sea posible usar el sistema de proyecciones de P que se muestra en la Figura 2, es necesario cambiar el ángulo entre los ejes temporales a:

$$\sin(\alpha)=\frac{x_2}{2ct_2}=v/2c.$$ (1)

Ahora podemos confirmar que el diagrama de espacio-tiempos Figura 2 es consistente con las transformaciones de Galileo:

$$x_2 = x_1 - v t_1,$$ (2)

$$t_2 = t_1.$$

Notar que la necesidad de que los ejes $x_1$ y $x_2$ sean paralelos viene del postulado Galileano que la simultaneidad de dos eventos es universal.

Figura 2: Los espacios-tiempos de O$_1$ y O$_2$

Pero grafiquemos ahora las lineas de mundo de dos rayos de luz: unos emitido por O$_1$, y el otro por O$_2$. Estas líneas corresponden a las bisectrices de los ángulos $\widehat{(x_1,ct_1)}$ y $\widehat{(x_2,ct_2)}$ (tarea: convencerse de esto). En la Figura 3, vemos que los dos rayos de luz tienen velocidades distintas en ambos referenciales. Es decir, en este diagrama la velocidad de la luz no es una constante universal.

Figura 3: Dos rayos de luz con velocidades distintas.

II Espacio-Tiempo, versión relativista.

En la Figura 3, para que se cumpla el segundo postulado de Einstein (la constancia de $c$), hubiese bastado con cambiar el eje $x_1$ de manera a que el rayo de luz de O$_2$ caiga también en la bisectriz del ángulo $(ct_,x_1)$. La Figura 4 ilustra esta idea. $ct_1$ es perpendicular a $x_2$, y $ct_2$ es perpendicular a $x_1$. De este modo el diagrama es equivalente para ambos observadores.

Figura 4: Un diagrama relativista: el rayo de luz es la bisectriz de los ejes temporales y espaciales de ambos observadores.

Falta determinar el ángulo $\alpha$, que elegimos de tal modo a poder usar la clásica regla de proyecciones para las coordenadas del evento P. Consideremos un evento en la linea de mundo de O$_2$ (en el eje $ct_2$), con coordenadas $(x_1,ct_1)$, vistas desde O$_1$:

$$\sin(\alpha)=\frac{x_1}{ct_1}=v/c.$$ (3)

Finalmente, hemos logrado construir un diagrama relativista, para lo cual la receta es (cambiando de notación de manera sugestiva: $x_2$ a $x$, y $x_1$ a $x^\prime$):

1. Graficar eje $c\hat{t}$, y normal a el, el eje $\hat{x}$.
2. Determinar $\alpha$ con $\sin(\alpha)=v/c$.
3. Graficar $c\hat{t^\prime}$, formando un ángulo $\alpha$ con el eje $c\hat{t}$.
4. Graficar el eje $\hat{x}$ perpendicular al eje $c\hat{t^\prime}$.

Dejamos como tarea deducir las transformaciones de Lorentz desde este típo de gráficos (llamados Diagramas de Loedel, 1948).

III Causalidad y v$<$c.

Consideremos dos eventos A y B conectados causalmente: A, un niño lanza una piedra a un vidrio, B, el vidrio se rompe. El diagrama espacio tiempo correspondiente está gráficado en la Figura 5. La pendiente de la linea que une A a B corresponde a una velocidad menor que $c$ (tarea: confirmarlo).

Figura 5: Una piedra es lanzada en A y rompe un vidrio en B.

Que sucede si la piedra es un tachyon que va más rápido que la velocidad de la luz? El diagrama podría ser el de la Figura 6. Vemos en este diagrama que $t_A<t_B$, mientras que $t_A^{\prime}<t_B^{\prime}$. De una manera general, si la linea que une dos eventos corresponde a una partícula movimiendose con velocidades mayor que $c$, siempre es posible encontrar un observador para el cual el efecto pasa a ser la causa. Como las relaciones causales estan a la base de la física, es imposible que $v>c$.

Figura 6: Un tachyon es lanzado en A y rompe un vidrio en B.