


Next: About this document ...
4
Problemas, radiación
Lámina con caras paralelas.
Iluminamos una lámina P con caras paralelas (i.e., una placa delgada
de vidrio), de espesor 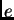 e índice de refracción
e índice de refracción 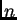 , gracias
a une fuente extendida emitiendo rayos luminosos
, gracias
a une fuente extendida emitiendo rayos luminosos 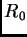 bajo varias
incidencias. Observamos en el plano focal de una lente
bajo varias
incidencias. Observamos en el plano focal de una lente 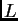 , de eje
perpendicular a la lámina
, de eje
perpendicular a la lámina 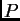 , un sistema de anillos circulares
obtenidos por interferencias de la vibración
, un sistema de anillos circulares
obtenidos por interferencias de la vibración 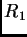 , directamente
reflejada sobre la primera cara de la lámina, y de la vibración
, directamente
reflejada sobre la primera cara de la lámina, y de la vibración
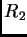 , reflejada por la segunda cara, como lo indica la Figura.
, reflejada por la segunda cara, como lo indica la Figura.
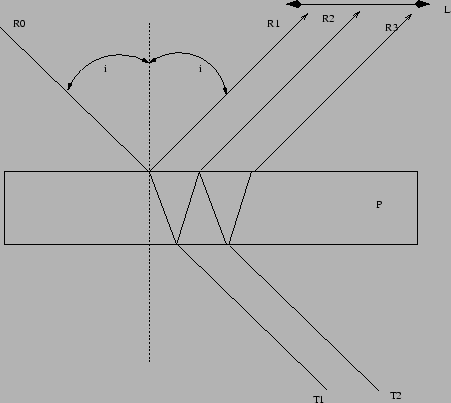
- Explicar la formación del sistema de interferencias (recordar
que la reflección en la primera cara induce un desfase de
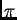 adicional al desfase asosciado a la diferencia de camino).
adicional al desfase asosciado a la diferencia de camino).
- La observación por transmisión permite ver un fenómeno
análogo?
- Que hay que pensar de las vibraciones siguientes, tales como
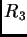 ?
?
Difracción por un rectángulo
Se perfora en una pantalla plana opaca 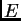 una apertura rectangular de
centro
una apertura rectangular de
centro 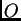 y de lados
y de lados 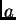 y
y 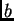 según los ejes
según los ejes 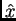 e
e
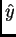 .
.
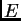 es iluminada bajo incidencia normal por luz monocromática de
longitud de onda
es iluminada bajo incidencia normal por luz monocromática de
longitud de onda 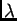 . Estudiamos la luz difractada sobre una
pantalla
. Estudiamos la luz difractada sobre una
pantalla 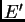 colocada en el plano focal de la lente
convergente
colocada en el plano focal de la lente
convergente 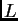 con un eje óptico confundido con
con un eje óptico confundido con 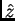 . Un punto
. Un punto
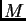 de
de 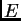 es ubicado por sus coordenadas
es ubicado por sus coordenadas 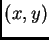 y un punto
y un punto
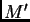 de
de 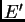 por sus coordenadas
por sus coordenadas
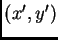 , en que los ejes
, en que los ejes
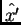 e
e
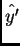 son paralelos a
son paralelos a 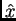 e
e 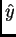 .
.
- Dar la expresión de la amplitud compleja de la onda difractada
por un elemento de superficie
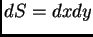 en la vecindad de
en la vecindad de 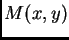 , y
en la dirección
, y
en la dirección 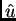 .
.
- Deducir la amplitud compleja de la onda difractada por la
apertura en dirección
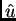 .
.
- Estudiar la iluminación en la pantalla
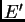 : calcular
: calcular
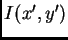 . Use como dato que rayos paralelos que
pasen por una lente convergente, convergen en un punto del plano
focal, en este caso
. Use como dato que rayos paralelos que
pasen por una lente convergente, convergen en un punto del plano
focal, en este caso 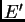 a una distancia
a una distancia 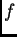 de la lente. Un
rayo que pase por el centro de la lente no es deflectado, y el punto
de convergencia de rayos paralelos esta determinado por la
intersección de un rayo que pase por el centro de la lente y el
plano focal.
de la lente. Un
rayo que pase por el centro de la lente no es deflectado, y el punto
de convergencia de rayos paralelos esta determinado por la
intersección de un rayo que pase por el centro de la lente y el
plano focal.
Difracción por una red
Construimos el montaje clásico de estudio de difracción en
infinito. La fuente 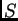 es una rendija infinitamente delgada, normal
al plano de la Figura, y ubicada en el plano focal de una lente
convergente
es una rendija infinitamente delgada, normal
al plano de la Figura, y ubicada en el plano focal de una lente
convergente 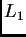 centrada en el eje óptico. Observamos el
fenómeno de difracción en el plano focal de una lente
centrada en el eje óptico. Observamos el
fenómeno de difracción en el plano focal de una lente 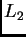 ,
centrada en el eje óptico del montaje, y cuya distancia focal es
,
centrada en el eje óptico del montaje, y cuya distancia focal es
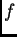 . En todo el problema, nos limiteramos al caso de rayos pocos
inclinados sobre el eje óptico. Entre las dos lentes
. En todo el problema, nos limiteramos al caso de rayos pocos
inclinados sobre el eje óptico. Entre las dos lentes 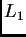 y
y 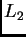 podemos colocar varios diafragmas
podemos colocar varios diafragmas 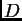 (pantallas con distintas
perforaciones) normales al eje óptico.
(pantallas con distintas
perforaciones) normales al eje óptico.
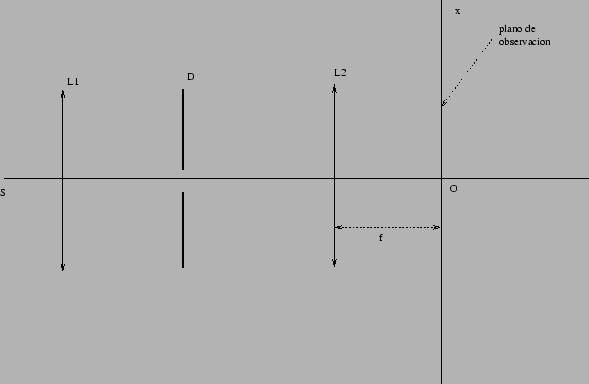
- La fuente luminosa
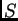 es monocromática de longitud de onda
es monocromática de longitud de onda
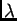 . El diafragma
. El diafragma 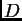 es constituido por dos rendijas identicas,
de ancho
es constituido por dos rendijas identicas,
de ancho 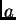 despreciable frente al largo de las rendijas, paralelas
entre ellas, cuyos separación es
despreciable frente al largo de las rendijas, paralelas
entre ellas, cuyos separación es 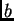 , y perpendiculares al plano de
la Figura (rendijas de Young).
, y perpendiculares al plano de
la Figura (rendijas de Young). 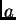 no es despreciable frente a
no es despreciable frente a
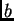 . Determinar la intensidad luminosa difractada en un punto
. Determinar la intensidad luminosa difractada en un punto 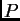 del
plano de observación en function de la distancia
del
plano de observación en function de la distancia 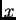 de ese punto a
la imagen geométrica
de ese punto a
la imagen geométrica 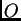 de la fuente
de la fuente 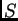 (en la intersección del
eje óptico y el plano de observación). La rendija fuente y las
rendijas de
(en la intersección del
eje óptico y el plano de observación). La rendija fuente y las
rendijas de 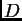 son de largo infinito, y sólo estudiaremos la
intensidad en función de
son de largo infinito, y sólo estudiaremos la
intensidad en función de 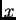 .
.
- dibujar la curva representando esta intensidad en función de
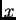 .
.
- El diafragma consiste ahora de
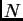 rendijas identicas y
paralelas, de ancho
rendijas identicas y
paralelas, de ancho 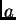 muy chico comparado con el largo de las
rendijas, y cuyos centros son distantes de
muy chico comparado con el largo de las
rendijas, y cuyos centros son distantes de 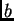 y perpendiculares al
plano de la Figura. Determinar el campo de intensidad obtenido en el
plano de observación.
y perpendiculares al
plano de la Figura. Determinar el campo de intensidad obtenido en el
plano de observación.
- El diafragrama en cuestión es una red por transmisión, con
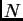 rendijas. Caracterisamos una red por la distancia entre dos
rendijas
rendijas. Caracterisamos una red por la distancia entre dos
rendijas 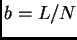 , si
, si 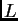 es el ancho total de la red. Para esta parte
del problema,
es el ancho total de la red. Para esta parte
del problema, 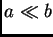 , de manera que se puede aproximar como constante
la componente de modulación del campo de intensidad debido al ancho
finito de las rendijas.
, de manera que se puede aproximar como constante
la componente de modulación del campo de intensidad debido al ancho
finito de las rendijas.
- determinar el ancho a zero intensidad de las imagenes de la
fuente
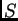 en el plano de observación (o sea el ancho de las
líneas de interferencias).
en el plano de observación (o sea el ancho de las
líneas de interferencias).
- la fuente
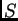 emite dos radiaciones de longitud de ondas vecinas
emite dos radiaciones de longitud de ondas vecinas
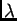 y
y
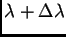 . Describir el fenómeno
observado. Consideramos que dos imagenes de
. Describir el fenómeno
observado. Consideramos que dos imagenes de 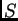 en el plano de
observación son distintas si, a lo menos, un máximo principal de
intensidad luminosa correspondiente a
en el plano de
observación son distintas si, a lo menos, un máximo principal de
intensidad luminosa correspondiente a 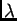 coincide con el
mínimo a zero intensidad de
coincide con el
mínimo a zero intensidad de
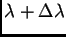 (o
inversamente). Deducir el poder de separación
(o
inversamente). Deducir el poder de separación
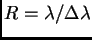 de la red de difracción.
de la red de difracción.
- Aplicación numérica:
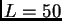 mm,
mm,
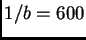 rendijas/mm. Determinar el ancho de cada imagen en el plano
de observación, y el poder de separación para el primer y el
segundo orden de interferencia (respuesta
rendijas/mm. Determinar el ancho de cada imagen en el plano
de observación, y el poder de separación para el primer y el
segundo orden de interferencia (respuesta 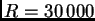 para el primer
orden).
para el primer
orden).
- Observamos unicamente en el primer orden de interferencia.
- Determinar el intervalo espectral
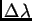 correspondiente, en el plano focal de
correspondiente, en el plano focal de 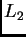 , a una distancia
, a una distancia 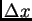 de los máximos de interferencia (despreciamos la envoltura de
difracción debida al ancho finito de cada rendija).
de los máximos de interferencia (despreciamos la envoltura de
difracción debida al ancho finito de cada rendija).
- el montaje descrito en este problema constituye un esquema
básico de un espectrógrafo de red; la cantidad
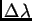 /
/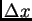 caracterisa la dispersión del sistema. La
dispersión se expresa en general en Angström por mm. Determinar,
en Å/mm, la dispersión del montaje, si la distancia focal
caracterisa la dispersión del sistema. La
dispersión se expresa en general en Angström por mm. Determinar,
en Å/mm, la dispersión del montaje, si la distancia focal 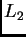 es
de 150mm. Respuesta:
es
de 150mm. Respuesta:
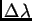 /
/
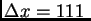 Å/mm.
Å/mm.
- Usamos ahora una fuente de luz blanca, es decir que emite en
todo el rango visible, desde
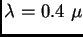 m a
m a
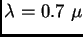 m.
Determinar la longitud ocupada en el plano focal por los espectros de
los tres primeros ordenes. Respuesta: en el primer orden,
m.
Determinar la longitud ocupada en el plano focal por los espectros de
los tres primeros ordenes. Respuesta: en el primer orden,
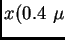 m
m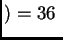 mm,
mm, 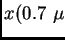 m
m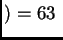 mm, y el ancho total es de
27 mm; para el segundo orden
mm, y el ancho total es de
27 mm; para el segundo orden 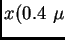 m
m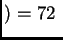 mm,
mm,
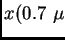 m
m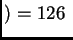 mm, y el ancho total es de 54 mm; para el tercer
orden
mm, y el ancho total es de 54 mm; para el tercer
orden 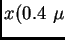 m
m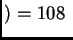 mm,
mm, 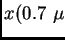 m
m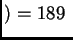 mm, y el ancho total
es de 91 mm.
mm, y el ancho total
es de 91 mm.
Que dificultad vamos a encontrar en la interpretación de los
espectros si observamos en ordenes superiores al primero? Ayuda: Hay
dos razones, una esta ligada con que si la red es realista, 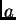 no es
despreciable delante de
no es
despreciable delante de 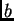 , y la otra esta ligada al ancho de cada
orden.
, y la otra esta ligada al ancho de cada
orden.
- Limitandosnos al primer orden, la aproximación de ángulos
pequeños es válida para todo el rango visible?



Next: About this document ...
simon
2002-05-28
![]() e índice de refracción
e índice de refracción ![]() , gracias
a une fuente extendida emitiendo rayos luminosos
, gracias
a une fuente extendida emitiendo rayos luminosos ![]() bajo varias
incidencias. Observamos en el plano focal de una lente
bajo varias
incidencias. Observamos en el plano focal de una lente ![]() , de eje
perpendicular a la lámina
, de eje
perpendicular a la lámina ![]() , un sistema de anillos circulares
obtenidos por interferencias de la vibración
, un sistema de anillos circulares
obtenidos por interferencias de la vibración ![]() , directamente
reflejada sobre la primera cara de la lámina, y de la vibración
, directamente
reflejada sobre la primera cara de la lámina, y de la vibración
![]() , reflejada por la segunda cara, como lo indica la Figura.
, reflejada por la segunda cara, como lo indica la Figura.

![]() una apertura rectangular de
centro
una apertura rectangular de
centro ![]() y de lados
y de lados ![]() y
y ![]() según los ejes
según los ejes ![]() e
e
![]() .
.
![]() es iluminada bajo incidencia normal por luz monocromática de
longitud de onda
es iluminada bajo incidencia normal por luz monocromática de
longitud de onda ![]() . Estudiamos la luz difractada sobre una
pantalla
. Estudiamos la luz difractada sobre una
pantalla ![]() colocada en el plano focal de la lente
convergente
colocada en el plano focal de la lente
convergente ![]() con un eje óptico confundido con
con un eje óptico confundido con ![]() . Un punto
. Un punto
![]() de
de ![]() es ubicado por sus coordenadas
es ubicado por sus coordenadas ![]() y un punto
y un punto
![]() de
de ![]() por sus coordenadas
por sus coordenadas
![]() , en que los ejes
, en que los ejes
![]() e
e
![]() son paralelos a
son paralelos a ![]() e
e ![]() .
.
![]() es una rendija infinitamente delgada, normal
al plano de la Figura, y ubicada en el plano focal de una lente
convergente
es una rendija infinitamente delgada, normal
al plano de la Figura, y ubicada en el plano focal de una lente
convergente ![]() centrada en el eje óptico. Observamos el
fenómeno de difracción en el plano focal de una lente
centrada en el eje óptico. Observamos el
fenómeno de difracción en el plano focal de una lente ![]() ,
centrada en el eje óptico del montaje, y cuya distancia focal es
,
centrada en el eje óptico del montaje, y cuya distancia focal es
![]() . En todo el problema, nos limiteramos al caso de rayos pocos
inclinados sobre el eje óptico. Entre las dos lentes
. En todo el problema, nos limiteramos al caso de rayos pocos
inclinados sobre el eje óptico. Entre las dos lentes ![]() y
y ![]() podemos colocar varios diafragmas
podemos colocar varios diafragmas ![]() (pantallas con distintas
perforaciones) normales al eje óptico.
(pantallas con distintas
perforaciones) normales al eje óptico.

![]() no es
despreciable delante de
no es
despreciable delante de ![]() , y la otra esta ligada al ancho de cada
orden.
, y la otra esta ligada al ancho de cada
orden.