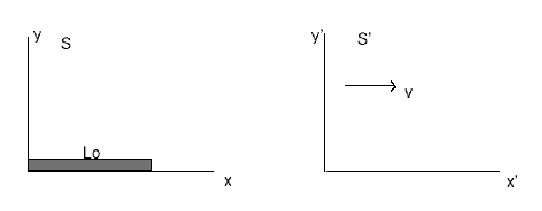Next: About this document ...
Problemas, relatividad especial
- Deducir las transformaciones de Lorentz suponiendo que
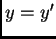 y
y 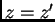 . Para identificar los coeficientes de la
transformacion lineal, usar el sistema de ecuaciones que deriva de los
siguientes experimentos:
. Para identificar los coeficientes de la
transformacion lineal, usar el sistema de ecuaciones que deriva de los
siguientes experimentos:
- El orígen de
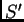 (en movimiento con respecto a
(en movimiento con respecto a 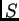 ),
tiene coordenas
),
tiene coordenas 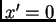 ,
, 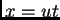 .
.
- Una señal radio es emitida en todas direcciones desde el
origen de
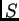 y
y 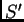 , que coinciden en
, que coinciden en 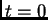 . El rayo de luz es
descrito por
. El rayo de luz es
descrito por
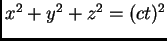 en ambos sistemas.
en ambos sistemas.
- Invertir la transformación de Lorentz, ver que es lo mismo que
llevar
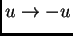 .
.
- Demostrar que la ecuación de ondas:
no es invariante ante una transformación de Galileo,
pero si ante una transformación de Lorentz.
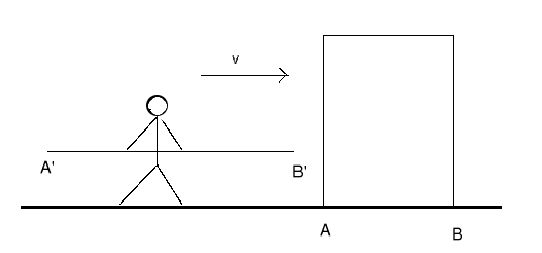
- Paradoja del garrochista y del granero. Una persona corre con
velocidad
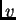 , tal que gamma es 2 respecto al granero, de largo 10m,
llevando con sigo una garrocha de largo 20m. Las puntas de la garrocha
se llaman
, tal que gamma es 2 respecto al granero, de largo 10m,
llevando con sigo una garrocha de largo 20m. Las puntas de la garrocha
se llaman 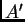 y
y 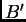 , y las puertas del granero se llaman
, y las puertas del granero se llaman
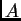 y
y 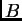 . Desde el punto de vista del granero se tiene la siguiente
secuencia de eventos:
. Desde el punto de vista del granero se tiene la siguiente
secuencia de eventos:
- la puerta
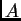 se abre al coincidir
se abre al coincidir 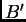 con
con 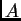 ,
,
- la puerta
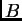 se cierra en forma simultánea con el evento 1.
se cierra en forma simultánea con el evento 1.
- la puerta
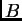 se abre al coincidir
se abre al coincidir 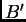 con
con 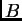 ,
,
- la puerta
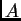 se cierra en forma simultánea con el evento 3.
se cierra en forma simultánea con el evento 3.
Explique com es posible esto, desde el punto de vista de la garrocha.
- Considere una barra en reposo de largo propio
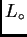 ubicada
en forma paralela al eje horizontal del sistema inercial
ubicada
en forma paralela al eje horizontal del sistema inercial 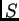 , tal como
se muestra en la figura. En
, tal como
se muestra en la figura. En 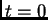 , la barra adquiere una velocidad
uniforme
, la barra adquiere una velocidad
uniforme
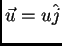 , la que mantiene en todo instante
posterior.
, la que mantiene en todo instante
posterior.
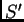 es otro sistema de referencia, coincidente con
es otro sistema de referencia, coincidente con 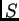 en
en
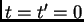 , que se mueve con velocidad uniforme
, que se mueve con velocidad uniforme
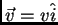 . Describir el movimiento de la barra en
. Describir el movimiento de la barra en
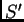 .
.



Next: About this document ...
simon
2002-03-21
 (en movimiento con respecto a
(en movimiento con respecto a 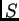 ),
tiene coordenas
),
tiene coordenas 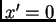 ,
, 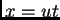 .
.
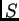 y
y 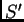 , que coinciden en
, que coinciden en 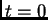 . El rayo de luz es
descrito por
. El rayo de luz es
descrito por
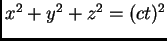 en ambos sistemas.
en ambos sistemas.
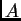 se abre al coincidir
se abre al coincidir 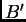 con
con 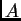 ,
,
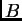 se cierra en forma simultánea con el evento 1.
se cierra en forma simultánea con el evento 1.
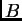 se abre al coincidir
se abre al coincidir 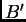 con
con 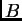 ,
,
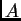 se cierra en forma simultánea con el evento 3.
se cierra en forma simultánea con el evento 3.