


Next: About this document ...
Propagación de ondas electromagnéticas en medios
dispersivos: Paquetes de ondas y velocidad de grupo
Repaso
Medio dispersivo
En los medio lineales y homogéneos, las ecuaciones de Maxwell se
modifican y la ecuación de onda se reemplaza por la ecuación de
propagación-absorpción, que es la ecuación de ondas con un término
disipativo:
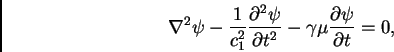 |
(5) |
con
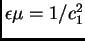 . Buscando soluciones en ondas planas
monocromáticas ,
. Buscando soluciones en ondas planas
monocromáticas ,
![\begin{displaymath}
\psi = \psi_{\circ} \exp[i(kx-\omega t)],
\end{displaymath}](img21.png) |
(6) |
obtenemos la relación del dispersión para el medio,
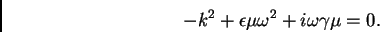 |
(7) |
Consideramos el caso en que la conductividad 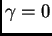 , o sea medios
aislantes (dielectricos, en los conductores las ondas son
evanescentes). Si
, o sea medios
aislantes (dielectricos, en los conductores las ondas son
evanescentes). Si 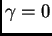 las soluciones del tipo
Ec. 6 ya fueron estudiadas para la ecuación de
ondas en el vacío. En el caso de los dielectrico, el índice
de refracción depende generalmente de
las soluciones del tipo
Ec. 6 ya fueron estudiadas para la ecuación de
ondas en el vacío. En el caso de los dielectrico, el índice
de refracción depende generalmente de 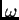 .
.
Pero soluciones como las ondas planas monocromáticas no son
físicas (se extienden hasta 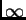 ), y para describir
perturbaciones localisadas formamos un paquete de ondas:
), y para describir
perturbaciones localisadas formamos un paquete de ondas:
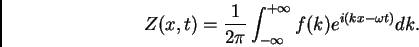 |
(8) |
Claramente, es Re![$[Z(x,t)]$](img25.png) que cobra sentido físico y que
describe la onda. En un medio dispersivo las soluciones de la
ecuación de propagación-absorpción son paquetes de ondas. Notar
que
que cobra sentido físico y que
describe la onda. En un medio dispersivo las soluciones de la
ecuación de propagación-absorpción son paquetes de ondas. Notar
que
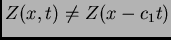 , porque
, porque 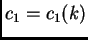 .
.
Como ejemplo, podemos formar un paquete de ondas que describa una
gaussiana para 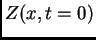 tomando un
tomando un 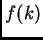 que también sea
gaussiano:
que también sea
gaussiano:
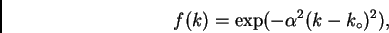 |
(9) |
que es una gaussiana con dispersión
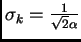 , y con la Ec. 8,
, y con la Ec. 8,
y finalmente
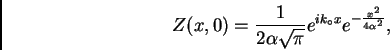 |
(11) |
o sea Re
![$[Z(x,0)] = \frac {1}{2\alpha \sqrt{\pi}}\cos(k_{\circ} x)
e^{-\frac{x^2}{4\alpha^2}}$](img37.png) .
.
Velocidad de grupo
Si 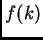 es una función localisada en torno a
es una función localisada en torno a 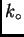 , podemos
expandir a primer orden
, podemos
expandir a primer orden
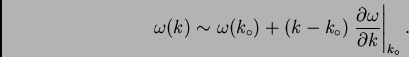 |
(12) |
Para ello, despreciamos
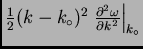 , lo cual es válido si la exponential decrece
suficientemente rápido. O sea, requerimos
, lo cual es válido si la exponential decrece
suficientemente rápido. O sea, requerimos
y vemos que la expansión Ec. 12 es válida sólo cuando
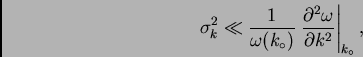 |
(14) |
es decir cuando 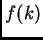 es suficientemente angosta.
es suficientemente angosta.
Con la expansion Ec. 12, el paquete de ondas
Ec. 8, se escribe
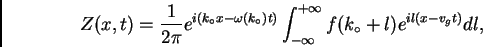 |
(15) |
en que definimos 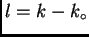 y la velocidad de grupo,
y la velocidad de grupo,
 |
(16) |
Finalmente,
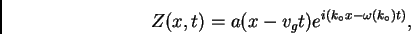 |
(17) |
donde 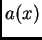 es la envoltura en
es la envoltura en 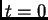 , que se propaga con
, que se propaga con 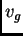 .
.
Dispersión del paquete de ondas
Si incluimos el término de segundo orden en la expansión
Ec. 12,
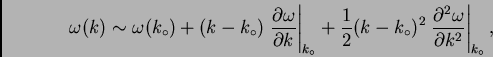 |
(18) |
tomamos
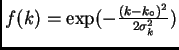 ,
después de un poco de cálculo obtenemos
,
después de un poco de cálculo obtenemos
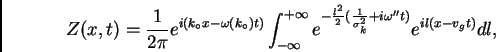 |
(19) |
con
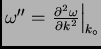 . Definiendo
. Definiendo
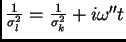 y
y
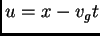 ,
,
Vemos que, si bien la expresión para Re![$[Z(x,t)]$](img25.png) es complicada, hay
una envoltura gaussiana con una dispersión que crece con el tiempo:
es complicada, hay
una envoltura gaussiana con una dispersión que crece con el tiempo:
![\begin{displaymath}
\mathrm{Re}[\sigma^2]=\frac{1}{\sigma_k^2}+(\omega^{\prime\prime}t)^2.
\end{displaymath}](img66.png) |
(21) |
En conclusión, el incluir el segundo orden en la expansión
Ec. 12 pone en evidencia que al transcurir el tiempo, se
enancha el paquete de ondas.



Next: About this document ...
simon
2002-05-27
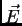 y
y
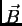 satisfacen la ecuación de ondas, que se puede escribir
genéricamente como:
satisfacen la ecuación de ondas, que se puede escribir
genéricamente como:
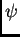 representa cada una de las componentes de
representa cada una de las componentes de 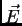 o
o
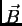 . Las soluciones de Ec. 1 son funciones
. Las soluciones de Ec. 1 son funciones 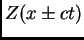 , o sea ondas propagandose hacia
, o sea ondas propagandose hacia 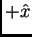 o
o 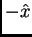 . En el
caso de una perturbación finíta, podemos descomponer
. En el
caso de una perturbación finíta, podemos descomponer 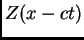 en sus
componentes espectrales:
en sus
componentes espectrales:
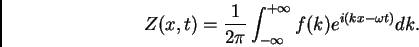
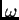 con
con 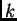 ), es simplemente
), es simplemente 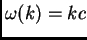 . La onda se
propaga sin deformarse con velocidad
. La onda se
propaga sin deformarse con velocidad 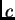 hacia
hacia 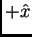 .
. 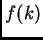 es
el espectro de la onda, que se puede ver como la superposicón de
componentes monocromáticas.
es
el espectro de la onda, que se puede ver como la superposicón de
componentes monocromáticas.
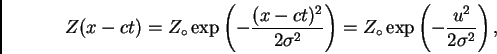
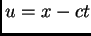 , entonces
, entonces
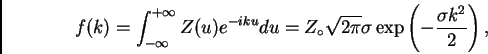
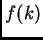 es otra gaussiana con dispersion
es otra gaussiana con dispersion
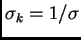 .
.
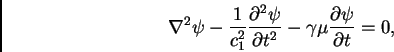
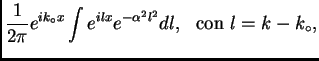
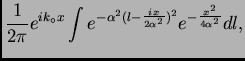

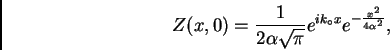
![$[Z(x,0)] = \frac {1}{2\alpha \sqrt{\pi}}\cos(k_{\circ} x)
e^{-\frac{x^2}{4\alpha^2}}$](img37.png) .
.
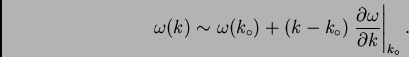
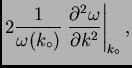
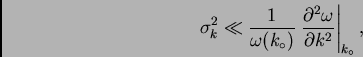

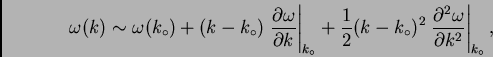
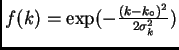 ,
después de un poco de cálculo obtenemos
,
después de un poco de cálculo obtenemos
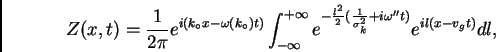
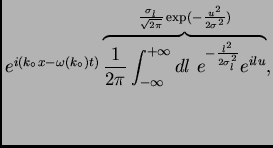
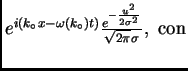
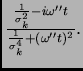
![\begin{displaymath}
\mathrm{Re}[\sigma^2]=\frac{1}{\sigma_k^2}+(\omega^{\prime\prime}t)^2.
\end{displaymath}](img66.png)